时间:2023-11-16 10:36:04
序论:在您撰写数学中的反证法时,参考他人的优秀作品可以开阔视野,小编为您整理的7篇范文,希望这些建议能够激发您的创作热情,引导您走向新的创作高度。
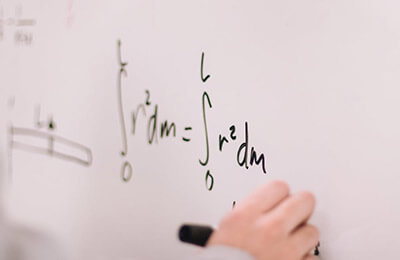
1 可以应用反证法的几类问题
1.1 某些具有唯一性的命题
在中学数学中,唯一性的问题比较常见,也是很平凡的一类数学问题,而要对于这些唯一性的命题加以论证,用我们常用的直接推理方法是很难证明的,也是不能直观启示我们解决这种问题,通过图形的启发,有利于得到证题的途径,那么解决这类问题最好的方法就是采用反证法,能够简便的证明唯一性的命题。
由此来看,在应用直接证明法证明问题时,要尽可能画出准确图形,这样可以通过图形的直观启示,有利于找到证明的途径,而反证法却恰好不同,它往往为了清楚地说明问题,常常需要画出某些不准确的图形,甚至不存在的图形,从而进行归谬证明,这就是反证法的基本特征之一。
1.2 结论为“不是”“不等”“不平行”或“必是”“必过”等否定或肯定的命题
在结论给予的是否定或肯定的命题时,通常采用直接法是很难得出证明途径的,就算能够经过分析法、综合法多种方法的合用能够加以证明,但证明过程相当复杂,而且难度很大,此时,我们通常采用“反证法”。
1.3 某些结论以“至多”“至少”等形式出现的命题
像“至多”或“至少”这样的问题,通常可以从相反的意义“至少”或“最多”来考虑问题,那么这类问题就简单多了。
1.4 用反证法证明“无限”类的命题
有些命题要证明结论中涉及“无限”的形式,如:要证明具有某种性质的元素有无穷多个,一般来说不容易直接证明的,而“无限”的反面是“有限”,以“有限”为前提进行推理论证就要方便多了。
综述,以上四种类型的问题,是中学数学中应用反证法最基本、最典型的几类问题。
2 反证法中怎样推出矛盾
2.1 与“反设”矛盾
例如:如图2-1所示,已知在ABC中,BEAC于点E,CFAB于点F,求证:AB=AC
证明:假设AB≠AC,若AB>AC,
SABC= AB・CF,
SABC=AC・BE,BE=CF,
AB・CF>AC・BE
即:SABC>SABC,这是个矛盾,
若AB
假设不成立,即:AB=AC
2.2 与“已知条件”矛盾
例如:如图2-2所示,在四边形ABCD中,AB+DB≤AC+CD,
求证:AB
证明:假设AB=AC,则在ABC中,
∠ACB=∠CBA,
但∠BCD>∠ACB,
∠BCD>∠CBD,
BD>CD,
BD+AB>CD+AC
这与已知条件AB+DB≤AC+CD相矛盾,
若AB>AC,在ABC中∠ACB>∠CBA,
又∠BCD>∠ACB
∠BCD>∠CBA 而∠CBA>∠CBD,
∠BCD>∠CBD BD>CD
AB+BD>AC+CD
与已知条件AB+DB≤AC+CD相矛盾
综述,AB≠AC,AB≯AC,AB
2.3 导致自相矛盾
例如:求证:方程8x+15y=50没有正整数解
证明:假设方程8x+15y=50有正整数解,x=x0,y=y0
则:8x0+15y0=50
8x0=50-15y0=5(10-3y0)5是8x0的约数,
因此,5是x0的约数,x0≥5
又8x0=50-15y0,y0是正整数,y0≥1,
8x0≤50-15=35
x0≤35/8 这与前面推出的x0≥5相矛盾,
故,方程8x+15y=50没有正整数解
2.4 推出与已知的定义、定理、公理、性质矛盾
例如:已知点A、B、C、D是平面内4个点,其中任意两个点不在同一条直线上,求证:总能在其中选出三个点,使其三点组成的三角形至少有一个不大于45°。
证明:假设在点A、B、C、D中任三点所构成的三角形的所有内角都大于45°,可分两种情况:
⑴ 若点A、B、C、D成凸四边形(如图右)则假设∠ABD、∠CBD、∠BAC、∠DAC、∠ADB、∠CDB、∠ACB、∠ACD都大于45°,
则:∠ABD+∠CBD+∠BAC+∠DAC+∠ADB+∠CDB+∠ACB+∠ACD>8×45°=360°,
即∠BAD+∠ABC+∠BCD+∠ADC>360°,
这与四边形的内角和为360°矛盾。
⑵ 若点A、B、C、D成凹四边形(如图2-4-2),连结AC、BD,假设∠ABD、∠ABC、∠ACB、∠ACD、∠ADC、∠ADB都大于45°,
则∠ABD+∠ABC+∠ACB+∠ACD+∠ADC+∠ADB>6×45°=270°,
即:∠DBC+∠BCD+∠CDB=270°
这与三角形的内角和为180°矛盾,
由⑴、⑵可知,命题得证。
在中学数学中,反证法中的矛盾大致由以上四种矛盾灵活组成,只要推出矛盾存在,则假设不成立。推出矛盾是反证法中的关键步骤,也是反证法中的必要步骤,通过矛盾来肯定结论。
3 总结中心论点及其反证法的错误使用和结果
反证法是中学数学中的证明方法之一,在中学数学应用中占有较高的地位,应用及其广泛,灵活运用反证法能够有效地解决某些数学问题,这就要求我们学会正确使用反证法,把反证法在数学中运用得灵活多变、自如。
何 昊
(江苏省南京市第十三中学锁金分校)
摘 要:系统地介绍了理论基础,对反证法的逻辑形式,唯一的负命题,命题,肯定命题三用反证法适用的命题类型进行了详细讨论。
关键词:反证法;否定性;唯一性
在数学的诸多方法中,反证法是一种重要的证明方法,尤其在数学证明中,它是一种间接的证据,被称为“一个最先进的武器”的数学家.反证法经常被用来证明存在性、否定性、唯一性等一些不易直接下手的命题.用反证法证明命题成立的基本步骤可以简单地概括为“否定―推理―反驳―肯定”四个步骤.一个数学问题的解决方案,如果你觉得不足或没有启动的“条件”,不妨考虑反证法的使用.反证法的应用范围很广,比如代数、数论、几何、组合等方面的应用.
一、反证法的概念及类型
反谓反证法,就是在要证明“若A则B”时,可以先将结论B予以否定,记作,然后从A与出发,经正确的逻辑推理而得到矛盾,从而原命题得证.
反证法大致可分为以下两种类型:
归谬法:论题结论的反面只有一种情况,只要把这种情况就达到了目的.
穷举法:论题结论的反面不止一种情况,要一一驳倒,最后才能肯定原命题结论正确.
二、反证法常用于以下几种命题的证明
1.存在性命题
例1:证明A,B,C,D,E五数之和等于5,则其中必有一个不小于1.
分析:这个问题似乎很简单,但直接的证明是不容易的.因此,应用反证法,它可以很容易地证明.
证明:假设A,B,C,D,E都小于1,那么A+B+C+D+E
所以5个数都小于1不成立,故必有一个数不小于1,即原命题是正确的.
2.否定性命题
例2:设平面上有六个圆,每个圆的圆心都在其余各圆的外部.试证明:平面上任一点都不会同时在这六个圆的内部.
分析:直接证明某点在哪些圆的内部,在哪些圆的外部,有些困难,故最好用反证法来证明.
证明:假设平面内有一点M同时在这六个圆的内部,为了方便,我们把绕M的六个圆心从某个开始按顺时针方向分别记为A,B,C,D,E,F,连结MA,MB,MC,MD,ME,MF.
考虑AMB,M在A内,B在A外,所以有AB>AM,同理,AB>BM,即在AMB中,AB大于其他两边.
由“大边对大角”知,∠AMB>∠ABM.同理,∠AMB>∠BAM.
所以,3∠AMB>∠ABM+∠AMB+∠BAM=180°,
所以∠AMB>60°.
同理∠BMC、∠CMD、∠DME、∠EMF、∠FMA均大于60°.
所以∠AMB+∠BMC+∠CMD+∠DME+∠EMF+∠FMA>360°.
但是,很显然,这个角围成了一个周角,它们的和不可能大于360°,出现矛盾.
故而假设不正确,所以原命题成立.
3.唯一性命题
例3:求证方程x=sinx+a(a为常数)的解唯一.
分析:直接解或证明是非常困难的,作为唯一的命题往往采用反证法证明.
所以原方程的解是唯一的.
从上面的例子中,我们可以看到,最大的优势是反证法――超过一个或几个条件,从相反的结论来看,与一些已知的条件下,原出口的冲突,从而达到负的假设、肯定原命题的目的.从上面,我们应该充分利用反证法,必须正确把握灵活运用“反设”“归谬”这两个反证步骤.反设是反证法的第一步,能否正确否定结论,对论证的正确性有着直接的影响.
反证法是很巧妙的,它的应用是很广泛的,但究竟怎样的命题证明才适于用反证法,却很难回答,这是一个经验问题.
参考文献:
[1]李建泉.中等数学[M].中国学术电子出版社,2004.
[2]刘广云.数学分析选讲[M].哈尔滨:黑龙江教育出版社,1993.
[3]张顺燕.数学的思想、方法和应用[M].北京:北京大学出版社,2003.
关键词: 中学数学教学 反证法 使用条件
在生活中,我们都有这样的常识,去掉大米中的砂粒,有两种方法.一种是直接从大米中把砂粒一粒一粒地拣出来;一种是用间接的方法――淘洗法,把砂粒残留下来.这两种方法虽然形式不同,但结果却是一样的,都能达到去掉砂粒的目的.有时用直接方法很困难,而用间接方法却容易得多.牛顿曾说:“反证法是数学家最精当的武器之一.”当一些命题不易从正面直接证明时,就可考虑用反证法.
一、反证法的基本概念
1.反证法的定义
法国数学家阿达玛对反证法的实质做了如下概括:“若肯定定理的假设而否定其结论,就会导致矛盾.”这是对反证法的极好概括.其实反证法也称作归谬法。反证法适合一些正面证明比较困难,但是否定则比较简单的题目,在高中数学中的应用较为广泛,在解决一些较难问题的时候,反证法能体现其优越性.
2.反证法的基本思想
反证法的基本思想就是否定之否定,这种基本思想可以用下面的公式表示:
“否定推理矛盾肯定”,即从否定结论开始,经过正确无误的推理导致逻辑矛盾,达到新的否定.
3.反证法的逻辑依据
通过以上三个步骤,为什么能肯定原命题正确呢?其逻辑根据就在于形成逻辑的两个基本规律:“排中律”和“矛盾律”.在同一思维过程中,两个互相矛盾的判断不能同时都为真,至少有一个是假的,这就是逻辑思维中的“矛盾律”;两个互相矛盾的判断不能同时都假,简单地说“A或者非A”,这就是逻辑思维中的“排中律”.反证法在其证明过程中,得到矛盾的判断,根据“矛盾律”,这些矛盾的判断不能同时为真,必有一假,而已知条件、已知公理、定理、法则或者已经证明为正确的命题都是真的,所以“否定的结论”必为假.再根据“排中律”,结论与“否定的结论”这一对立的互相否定的判断不能同时为假,必有一真,于是我们得到原结论必为真.所以反证法是以逻辑思维的基本规律和理论为依据的,反证法是可信的.
二、反证法的步骤
用反证法证题一般分为三个步骤:
1.反设.假设原命题的结论不成立;
2.归谬.从这个结论出发,经过推理论证,得出矛盾;
3.结论.由矛盾判定假设不成立,从而肯定原命题的结论正确.
即:否定结论推导出矛盾结论成立.
三、反证法的种类
1.归谬反证.结论的反面只有一种情形,只要把它驳倒,就能达到证题目的.
2.穷举反证.结论的反面不止一种情形,必须将它们逐一驳倒,才能达到证题目的.
四、反证法的典型例题
例1:已知:AB,CD是圆内非直径的俩弦(如图),求证:AB与CD不能互相平分.
证明:假设AB与CD互相平分与点M,则由已知条件AB,CD均非圆O直径,可以判定M不是圆心O,联结OA,OB,OM.
因为OA=OB,M是AB中点,所以OMAB(等腰三角形底边上的中线垂直于底边).同理可得:OMCD,从而过点M有两条直线AB,CD都垂直于OM.这与已知的定理相矛盾.故AB与CD不能互相平分.
五、反证法的使用条件
任何方法都有它成立的条件,也都有它适用的范围.离开了条件超越了范围就会犯错误,同样,问题解决也就没有那么容易.因此,我们应该学会正确使用反证法解题.
虽然用反证法证明,逻辑推理严谨而清晰,论证自然流畅,可谓是干净利落,快速而可行,是一种很积极的证明方法,而且用反证法证题还有很多优点:如思想选择的余地大、推理方便等.但是并不是什么题目都适合用反证法解决.
例2:如果对任何正数p,二次方程ax+bx+c+p=0的两个根是正实数,则系数a=0,试证之.
分析:看了本题的证明过程似乎很合理,但其实第三步,即肯定原结论成立的论证错了.因为,本题的题设条件为对任意正数p,y=0有两个正实数根,结论是a=0,但本题的题设条件与结论是矛盾的;当a=0时,二次方程就变成了一次方程bx+c+p=0,此一次方程在b≠0时,对于任何正数p,它只有一个根;在b=0时,仅当p=-c>0的条件下,它有无数个根,否则无根,但总之不会有两个根.题设条件和结论矛盾.因此,本题不能反证法来处理.若原题改为“如果对于任何正数p,只存在正实根,则系数a=0”,就能用反证法证明.
因此,对于下列命题,较适用反证法解决.
(1)至多至少型命题;(2)唯一性命题;(3)否定型命题;(4)明显型命题;(5)此前无定理可以引用的命题.
例3:设a,b都是正数,求证:(a-b)/a≤ln(a/b)≤(a-b)/b.
证明:反设ln(a/b)≤(a-b)/b不成立,便有ln(a/b)≥(a-b)/b,由对称性知:ln(b/a)≥(b-a)/a,相加得:ln(a/b)+ln(b/a)>(a-b)/b+(b-a)/a
即:0>(a-b)/a≥0这一矛盾说明ln(a/b)≤(a-b)/b
即:ln(b/a)≥(a-b)/b
交换位置:ln(a/b)≥(a-b)/b
合并得:(a-b)/a≤ln(a/b)≤(a-b)/b
反证法是数学中的一种重要的证明方法.牛顿曾说:“反证法是数学家最精当的武器之一.”它是从命题的否定结论出发,通过正确的逻辑定理推理导出矛盾,从而证明原命题的正确性的一种重要方法.反证法之所以有效是因为它对结论的否定实际上增加了论证的条件,多一个条件,这对发现正确的解题思路是有帮助的.对于具体、简单的命题;或者直接证明难以下手的命题,改变其思维方向,通过逆向思维,从结论入手进行反面思考,问题就能迎刃而解.在现代数学中,反证法已成为最常用和最有效的解决问题的方法之一.
参考文献:
[1]赵振威.中学数学教材教法[M].华东师范大学出版社,2000.
[2]刘世泽.反证法的逻辑依据[J].高等函授学报,1997(4).
[3]耿素云.离散数学[M].北京:高等教育出版社,1998.
[4]赵杰.反证法―――化难为易的法宝.中学生数理化(高二版),2010,(3).
[5]路从条.“反证法”思想在中学教学中的运用.福建教育学院学报,2003,(3).
关键词:反证法;证明;矛盾;命题;假设
有个很著名的“道旁苦李”的故事:从前有个名叫王戎的小孩,一天他和小朋友发现路边的一棵树上结满了李子,小朋友一哄而上,去摘,尝了之后才知是苦的,独有王戎没动,王戎说:“假如李子不苦的话,早被路人摘光了,而这树上却结满了李子,所以李子一定是苦的。”这个故事中王戎用了一种特殊的方法,从反面论述了李子为什么不甜,不好吃.在数学里这种方法叫反证法.
反证法不但在实际生活和初等数学中有着广泛的应用,而且在高等数学中也具有特殊作用.数学中的一些重要结论,从最基本的性质、定理,到某些难度较大的世界名题,往往是用反证法证明的.即:提出假设――推出矛盾――肯定结论.
“反证法”虽然是在平面几何教材中出现的,但对数学的其他各部分内容,如代数、三角、立体几何、解析几何中都可应用.下面通过具体的例子来说明其应用。
一、否定性命题
证明:假设AB,CD不平行,即AB,CD交于点P,则过P点有ABEF,且CDEF,与“过直线外一点,有且只有一条直线垂直于已知直线”矛盾.假设错误,则AB∥CD
否定结论导出矛盾是反证法的任务,但何时出现矛盾,出现什么样的矛盾是不能预测的,也没有一个机械的标准,有的甚至是捉摸不定的.一般总是在命题的相关领域里考虑(例如,平面几何问题往往联系到相关的公理、定义、定理等),这正是反证法推理的特点.因此在推理前不必要也不可能事先规定要得出什么样的矛盾.只需正确否定结论,严格遵守推理规则,进行步步有据的推理,矛盾一经出现,证明即告结束.
反证法推理过程中出现的矛盾是多种多样的,推理导出的结果可能与题设或部分题设矛盾,可能与已知真命题(定义或公理、或定理、或性质)相矛盾,可能与临时假设矛盾,或推出一对相互矛盾的结果等.
关键词:反证法;数学;证明
【中图分类号】G633.6
1 引言
公元前六世纪中期的古希腊七贤之首--泰勒斯最早引入了数学证明的思想,公元前三世纪的古希腊数学家欧几里德第一个最广泛、最娴熟地运用了数学证明,我国数学家江泽函则指出:"没有数学证明,就没有数学"。反证法是数学证明中的一种间接证明方法,在数学命题的证明中被广泛应用。欧几里德证明"素数有无穷多"、欧多克斯证明"两个正多边形的面积比等于其对应线段比的平方"、"鸽子原理"和"最优化原理"的证明等都用了反证法。但是由于在现行的各种教材中没有对反证法给出系统的介绍,学生对反证法原理的理解和恰当地运用也存在不少的问题,故本文在此"抛砖引玉"。
2 反证法内涵
2.1 什么是反证法
法国数学家阿达玛说过:"反证法在于表明,若肯定定理的假设而否定其结论,就会导致矛盾。"即先假设命题中结论的反面成立,结合已知的定理条件,进行正确的推理、论证,得出和命题中的题设或前面学习过的定义、公理、定理、已知的事实相矛盾,或自相矛盾的结果,从而断定命题结论的反面不可能成立,因而断定命题中的结论成立,这种证明的方法就叫做反证法。
2.2 反证法的原理
2.2.1 矛盾律
矛盾律是亚里士多德的形式逻辑的基本规律之一,其基本内容是:在同一个论证过程中,对同一对象的两个相矛盾的、对立的判断,其中至少有一个是假的,它的公式是:不是。如对""这个对象,"是有理数"和"是无理数"的两个判断中至少有一个是假的。
2.2.2 排中律
排中律是形式逻辑的由一个基本规律,其基本内容是:在同一个论证过程,对同一对象的肯定判断和否定判断。这两个相矛盾的判断必有一个是真的,它的公式是:或者是或者是,排除了第三种情况的可能,在数学论证中常根据排中律进行推理。如要证明"是有理数",只要证明"不是有理数"不真就够了。这是因为"不是有理数"和"是有理数"是对象的两个相矛盾的判断,根据排中律,其中必有一个是真的。
2.3 运用反证法证明论题的步骤
运用反证法证明数学命题"",首先,必须弄清楚命题的条件和结论,然后按以下步骤进行论证:
第一步:否定命题的结论,作出与相矛盾的判断,得到新的命题;
第二步:由出发,利用适当的定义、定理、公理进行正确的演绎推理,引出矛盾结果;
第三步:断定产生矛盾的原因,在于判断不真,从而否定,肯定原结论成立,间接证明了原命题。
分析上述三个步骤可以发现,运用反证法的关键在于由新的论题演绎出一对矛盾,一般为推出的结果与某一定义、定理、公理、已知条件、所作题断矛盾,或是推出两个相互矛盾的结果。
值得注意的是在运用反证法证明命题时要认真细致地审题,若发现与论题结论相矛盾方面有不止一种情况,必须予以一一否定。且有时并非全部运用反证法,它可能只在证明过程中部分地出现。
3 反证法在证明论题中的运用
反证法是重要的证明方法,在几何、代数等领域都有广泛的运用,现分类举例说明。
3.1 反证法在几何中的运用
3.2 反证法在代数中的运用
4 结语
由上可知,用反证法证明一些问题时,有着其它方法所不能替代的作用。师生在了解了反证法的特点、证明过程及应用"须知"后,加强训练、不断总结,就能熟练地运用了。
参考文献:
[1] 杜永中.反证法[M].四川:四川教育出版社,1989:20.
[2] 黄志宁.谈谈反证法[J].福建商业高等专科学校学报,2000,20(4):24-25.
关键词:反证法;证明;矛盾;应用
中图分类号:G633.6?摇 文献标志码:A 文章编号:1674-9324(2014)02-0077-02
在中学数学中,反证法应用相当广泛。怎样正确运用反证法是一个难题。本文主要研究的是一些直接证明难以入手甚至无法入手的题目,用反证法就会使证明变得轻而易举。
一、反证法原理及解题步骤
1.反证法原理。反证法是一种论证方式。它首先假设某命题不成立,然后推出明显矛盾的结论,从而得出原假设不成立,原命题得证。总的来说反证法就是通过证明原命题的反面不成立来确定原命题正确的一种证明方法。反证法在中学数学中经常运用。有的问题不易从问题的正面去解答,但若从问题的反面着手却容易解决,它从否定结论出发,经过正确严格的推理,得到与已知假设或已成立的数学命题相矛盾的结果,从而得到原命题的结论是不容否定的正确结论。
2.反证法的解题步骤。在中学数学题目的求解证明过程中,当直接证明一个命题感到困难时,我们经常采用反证法的思想。由此,我们总结出用反证法证明命题的三个步骤:①提出假设:做出与求证结论相反的假设。②推出矛盾:与题设矛盾;与假设矛盾;恒假命题。③肯定结论:说明假设不成立,从而肯定原命题成立。数学问题是多种多样的,尽管大多问题一般使用直接证明,但有些问题直接证明难度较大,而用反证法证明,却能迎刃而解。下面我们结合实例总结几种常用反证法的情况。
二、反证法在中学数学中的应用
反证法虽然是在平面几何教材中提出来的,但对数学的其他部分内容如代数、三角函数、立体几何、解析几何中都可应用反证法。那么,究竟什么样的命题可以用反证法来证呢?下面就列举几种一般用反证法来证比较方便的命题。
1.基本命题。基本命题就是学科中的起始性命题,这类命题由于已知条件及能够应用的定理、公式、法则较少,或由题设条件所能推出的结论很少,因而直接证明入手较难,此时应用反证法容易奏效。
例1 求证:两条相交直线只有一个交点。已知:如图,直线a、b相交于点P,求证:a、b只有一个交点。证明:假定a,b相交不只有一个交点P,那么a,b至少有两个交点P、Q。于是直线a是由P、Q两点确定的直线,直线b也是由P、Q两点确定的直线,即由P、Q两点确定了两条直线a,b。
与已知公理“两点只确定一条直线”相矛盾,则a,b不可能有两个交点,于是两条相交直线只有一个交点。
2.否定性命题。否定性命题,也就是结论以否定形式出现的命题,即结论以“没有……”“不是……”“不能……”等形式出现的命题,直接证法一般不易人手,而运用反证法能使你见到“柳暗花明又一村”的景象。
3.存在性问题。在存在性问题中,结论若是“至少存在”,其反面是“必定不存在”,由此来推出矛盾,从而否定“必定不存在”,而肯定“至少存在”。我们用反证法来证明。
例2 已知x∈R,a=x2+0.5,b=2-x,c=x2-x+1求证:a,b,c中至少有一个不小于1。证明:假设a,b,c都小于1,则2x2-2x+3.5
4.无穷性命题。无穷性命题是指在求证的命题中含有“无穷”、“无限”等概念时,从正面证明往往无从下手时,我们常使用反证法。
例3 证明■是无理数。证明:假设■不是无理数,那么■是有理数,不妨设■=■(m,n为互质的整数), m2=3n2,即有m是3的倍数,又设m=3q(q是整数),代人上式得n2=3q2,这又说明n也是3的倍数,那么m与n都是3的倍数,这与我们假设m、n互相矛盾,■是无理数。
5.唯一性命题。有关唯一性的题目结论以“…只有一个…”或者“……唯一存在”等形式出现的命题,用反证证明,常能使证明过程简洁清楚。
例4 设0
从而|x1-x2|≤2bsin(x1-x2)/2≤2b(x1-x2)/2=b|x1-x2|,即 |x1-x2|≤b|x1-x2|,此与x1≠x2且0
三、应用反证法应该注意的问题
对于同一命题,从不同的角度进行推理,常常可以推出不同性质的矛盾结果,从而得到不同的证明方法,它们中有繁冗复杂,有简单快捷,因此,在用反证法证明中,应当从命题的特点出发,选取恰当的推理方法。
1.必须正确“否定结论”。正确否定结论是运用反证法的首要问题。
2.必须明确“推理特点”。否定结论导出矛盾是反证法的任务,但出现什么样的矛盾是不能预测的。一般是在命题的相关领域里考虑,这正是反证法推理的特点。只需正确否定结论,严格遵守推理规则,进行步步有据的推理,矛盾一出现,证明即告结束。
3.了解“矛盾种类”。反证法推理过程中出现的矛盾是多种多样的,推理导出的结果可能与题设或部分题设矛盾,可能与已知真命题(定义或公理、或定理、或性质)相矛盾,可能与临时假设矛盾,或推出一对相互矛盾的结果等。
反证法是一种简明实用的数学解题方法,也是一种重要的数学思想。学会运用反证法,它可以让我们掌握数学逻辑推理思想及间接证明的数学方法,提高观察力、思维能力、辨别能力,以及养成严谨治学的习惯。我认为,只有了解这些知识,在此基础上再不断加强训练,并不断进行总结,才能熟练运用。
参考文献:
[1]陈志云,王以清.反证法[J].高等函授学报(自然科学版),2000,13(6):20-23.
[2]阎平连.浅谈反证法在初中数学中的运用[J].吕梁高等专科学校学报,2002,18(1):28-29.
[3]张安平.反证法――证明数学问题的重要方法[J].教育教学,2010,1(11):179-180.
[4]张世强.浅析“反证法”[J].成都教育学院学报,2000,6(06):09-10.
关键词:反证法;数学教学;应用
反证法是一种重要的证明方法,历来是教学中的重点和难点。运用反证法有时可以达到简练又确切的良好效果,可以说,没有反证法的数学,只是原始、极不完整的数学,因此,深刻的理解反证法的实质,了解这种方法的一般规律,对于提高逻辑思维能力和解决实际问题的能力,有着十分重要的意义。本文通过以下方面来说明反证法在教学中的应用。
一、什么是反证法
反证法是一种间接证明命题的方法。该方法先提出与结论相反的假设,然后以此及其有关的定义、公理、定理、题设为依据,言出有据地导出矛盾的结果,从而证明了与结论相反的假设不能成立,进一步肯定原来的结论必定成立。简言之,就是从反面人手论证命题的真实性的方法。
反证法具体又分为归谬法和穷举法,在反证法中,当命题的结论的反面只有一个时,则只需这种情况就能证明结论正确,这种反证法叫做“归谬法”。当命题结论的反面有两种或两种以上的可能时,则需一一,从而肯定原结论为真,这种反证法叫做“穷举法”。
二、反证法的证题步骤
运用反证法证题时,一般有下述三个步聚:
(1)反设:就是假设原命题的结论的反面成立。
(2)归谬:从假设出发,由正确的演绎推理过程,推出与公理,或定义,或与已知定理和公式,或与已知条件,或与假设相矛盾的结果,或所推得的结果自相矛盾。
(3)结论:判断原命题结论反面不能成立,从而肯定原命题结论成立。
三、宜用反证法证明的命题形式
为了便于运用反证法证题,必须搞清宜用反证法证明的命题所具有的以下几种常见形式。
待证命题用直接法难于人手时,宜用反证法.如立体几何中开始的一些性质定理的证明就是如此。
下面再举一例
例1 如果正实数a,b满足ab=ba,且a
证:假设a≠b,即ab
ab=bablna=alnb,
这与(1)式相矛盾,故a>b的假设不成立
所以,有a=b
说明:此题用反证法,推出结论与题设相矛盾,并及时地发现矛盾。
四、反证法证题时,应注意的问题
(1)一定要在推理过程中有意地制造矛盾,并及时地发现矛盾。